bassale.blogg.se - Half adder truth table to circuit

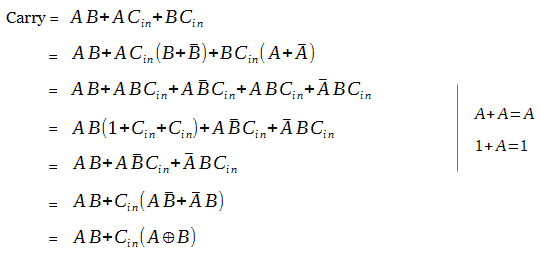
HALF ADDER TRUTH TABLE TO CIRCUIT HOW TO
HALF ADDER TRUTH TABLE TO CIRCUIT FULL
HALF ADDER TRUTH TABLE TO CIRCUIT SERIES

We can also add multiple bits binary numbers by cascading the full adder circuits. But in Full Adder Circuit we can add carry in bit along with the two binary numbers. In half adder we can add 2-bit binary numbers but we cant add carry bit in half adder along with the two binary numbers. Mainly there are two types of Adder: Half Adder and Full Adder. As in binary number system, 1 is the largest digit, we only produce carry when the addition is equal or greater than 1 + 1 and due to this, carry bit will be passed over next column for addition. These two numbers can represent SUM or CARRY or both. In binary, we only get two numbers either 1 or 0. Instead of the two denary numbers here binary numbers are used. In case of binary number addition the process is same. So, each value has a weighted value based on its column position. We wrote 0 and carry the 1 to the next column.

HALF ADDER TRUTH TABLE TO CIRCUIT HOW TO

In the next tutorial, we’ll learn how to design half and full subtractor circuits using VHDL.We add each column from right to left and if the addition greater than or equal to 10, we use carry. In the above figure, one case is highlighted as a=1, b=1, and cin=0, with the outputs of sum=0 and carry=1. architecture of full adder-Ĭompare the outputs “sum” and “carry” with the given truth table. (The full-adder circuit consist of two half adder and one OR gate). We’ll build a full-adder circuit using the “ half-adder circuit” and the “ OR gate” as components or blocks. Here, we’ll also use that style rather than the data-flow modeling style. In the previous tutorial, we designed one Boolean equation digital circuit using a structural-modeling style of the VHDL programming. Let’s write a VHDL program for this circuit. Next, let’s move on to the full adder circuit and its design. For the a=1 and b=0 inputs, the outputs are sum=1 and cry=0, which are highlighted in the figure. Verify the ‘sum’ and ‘cry’ output waveforms with the given truth table. Next, compile the above program, creating a waveform file with all of the necessary inputs and outputs that are listed, and simulate the project. To refresh your memory about how this works, go through the first two VHDL tutorials ( 1 and 2) of this series.

“ architecture ” describes the operation of the circuit, which refers to how the output is generated from the given input.

As per the circuit given above, we have two inputs ‘a,’ ‘b,’ and two outputs, ‘sum’ and ‘cry.’

“ entity ” describes the input-output connections of the digital circuit.

In that tutorial, we learn how to design a project, edit and compile a program, create a waveform file, simulate the program, and generate the final output waveforms. However, first it’s important to review the step-by-step procedure provided in VHDL Tutorial – 3. We’ll also verify the output waveforms with the given truth table. Now, we’ll write a VHDL program, compile and simulate it, and get the output in a waveform.

Verify the output waveform of the program (digital circuit) with the half and full-adder circuits’ truth tables.

Write a VHDL program to build half and full-adder circuits.In the previous tutorial VHDL Tutorial – 9, we learned how to build digital circuits from given Boolean equations.

HALF ADDER TRUTH TABLE TO CIRCUIT SERIES

Note: it’s recommended to follow this VHDL tutorial series in order, starting with the first tutorial.